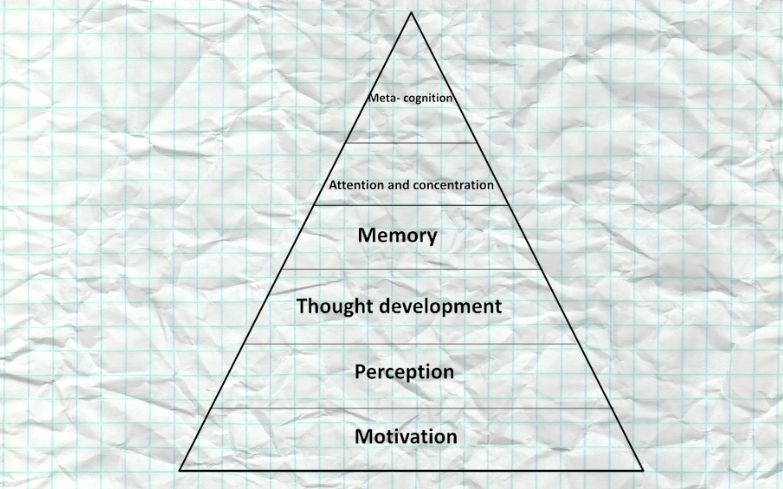
משהו קורה שם לתלמידים בערך בגיל 10, אחרי שדיקלמו באופן רהוט את לוח המאה ופותרים שאלות בתחום האלפים, ההורים מתמלאים בגאווה – ואז זה מגיע. מי לא זוכר את הפיצה הנחלקת לחלקים ברמה חזותית בהירה – ובכל זאת, כשמדובר על שברים, יעידו מאובחנים בחשבון שזו נקודת השבר: למידת שברים נתפסת כ"אירוע מכונן".
בשנים האחרונות כתבה ד"ר איריס שביט על חרדה ולקות מתמטית וניסתה באמצעות כלים מחקריים, לאתר את הנקודה בה התלמיד הפסיק להאמין בעצמו. בנקודה זו, עולות בראשו של התלמיד מחשבות אפילו לנטוש את המקצוע האימתני והקר. בדרך כלל מלווה לכך תמונת זיכרון של מורה שלא מסתדר איתו בלשון המעטה.
אז בואו ננסה לפרק וזה מה שצריך לעשות בכל תוכן לימודי. לשאול את עצמנו: איך זה נתפס בעיני התלמיד?
ד"ר איריס שביט מעלה כאן מספר קשיים:
- מעבר ממספר יחיד אופקי לצורה אנכית עם קו שבר: לאחר שנים שהתלמיד נחשף למספרים ארוכים ככל שיהיו בצורה אופקית, הוא פוגש לראשונה במערכת של שלושה סמלים: מספרים בטור אנכי וקו ביניהם – רמת הקונקרטיות שלהם נמוכה וקשה לעיכול.
- הבנת ההבדל בין מספר שלם לחלקיות: בתוך עומס הפרטים, הוא גם צריך להבין ברוב המקרים שאין זה מספר שלם. זו הסחרחורת הראשונה בראשו. מה שנקרא חרדה מתמטית חלקית.
- חילוק שונה ממה שהכרנו: קו השבר כמחלק. התלמידים צריכים להבין, שמדובר לא רק על מספר שאינו שלם, אלא נחלק במכנה. מה קורה לתלמיד שמנסים להסביר לו חלוקת 2 ב-5?